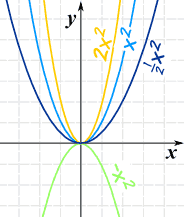
Similarly, the graph of y = x 2 3 is 3 units below the graph of y = x 2 The constant term "c" has the same effect for any value of a and b Parabolas in the vertexform or the ahk form, y = a(x h) 2 k To understand the vertexform of the quadratic equation, let's go back our orginal equation, f(x) = x 2 In this equation, remember This video shows how to use horizontal and vertical shifts together to graph a radical functionThe graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 k where a ≠ 0 The vertex (h, k) is located at h = – b 2a, k = f(h) = f

Graph Quadratic Functions Using Transformations Intermediate Algebra
What is the vertex of the graph f(x)=y=a(x-h)2+k
What is the vertex of the graph f(x)=y=a(x-h)2+k-The quadratic function $f(x)=a(xh)^{2}k$ is in standard form (a) The graph of is a parabola with vertex (b) If $a>0,$ the graph of $f$ opens _____ In this case $f(h)=k$ is the _____ value of $f$ (c) If $a F(x) = f(x) − k Table 251 Example 251 Sketch the graph of g(x) = √x 4 Solution Begin with the basic function defined by f(x) = √x and shift the graph up 4 units Answer Figure 253 A horizontal translation 60 is a rigid transformation that shifts a graph left or right relative to the original graph




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation
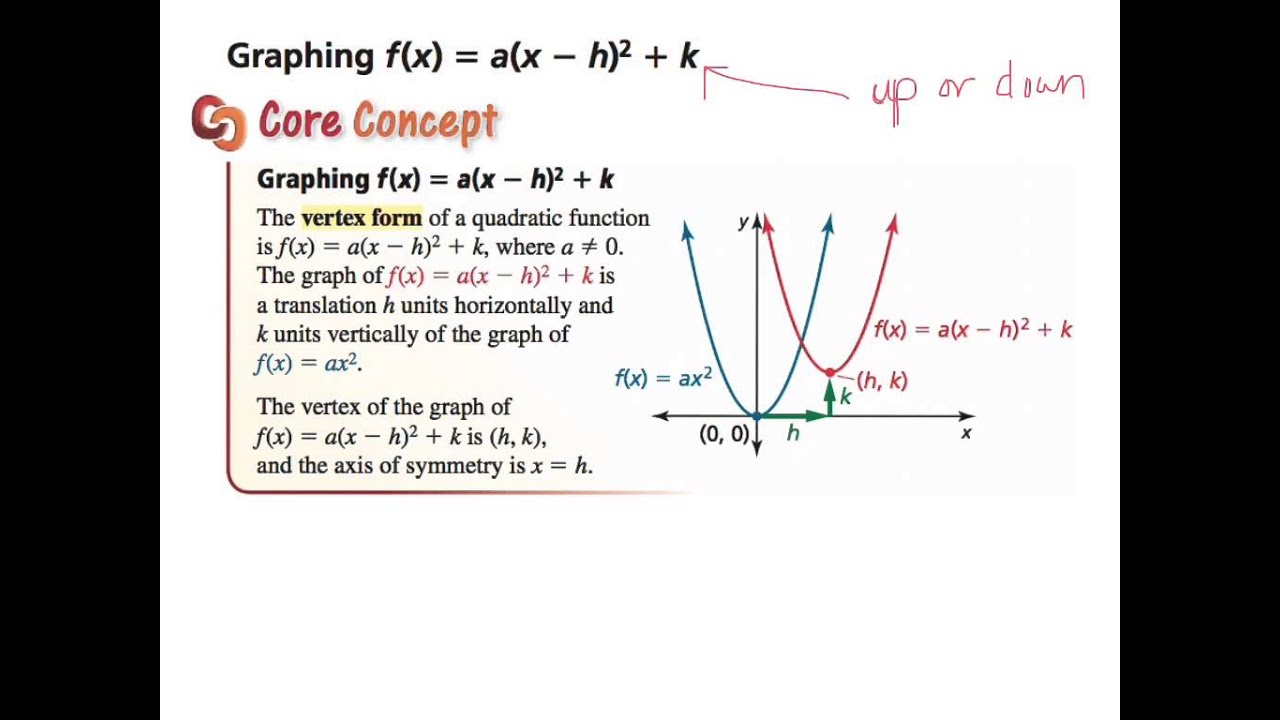
Graphing f (x) = a(x − h)2 k CCore ore CConceptoncept Graphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − h)2 k is (h, k),The standard form of a quadratic function is f(x) = a(x h) 2 k, a ≠ 0 1 It is always a cupshaped curve 2 It opens upward if a > 0 and opens downward if a < 0 3 The vertex is at (h, k) and the axis of the function is at x = h 4 (h, k) is a maxima if a < 0 and aHere is the graph of y = a ( x − h) 2 k Use the sliders to change the values of a, h, and k so that you are looking at the graph of y = 2 ( x − 1) 2 2 Fill in the following table (The equation for the graph is written below the grid) Equation
Answer to Describe the graph of f(x) = a(xh)^2 k when a = 0 Is the graph the same as that of g(x) = ax^2 bxc when a=0?How to graph a quadratic function using horizontal shiftsMake sure to show the graph INSERT don t ATTACH ;
Learn how to graph in vertex form!C) f(x) = 2(x 3) 2 = 2(x 3)) 2 0 a = 2 , h = 3 and k = 0 The vertex is at (3,0) and it is a minimum point since a is positive Interactive Tutorial Use the html 5 (better viewed using chrome, firefox, IE 9 or above) applet below to explore the graph of a quadratic function in vertex form f(x)=a (xh) 2 k where the coefficients a, h The function p(x) = –8x2 – 64x can be written in vertex form p(x) = a(x – h)2 k, where a =, h =, and k = To graph the function p, reflect the graph of f(x) = x2 across the xaxis, vertically stretch the graph by a factor of 8, shift the graph units, and then shift the graph units
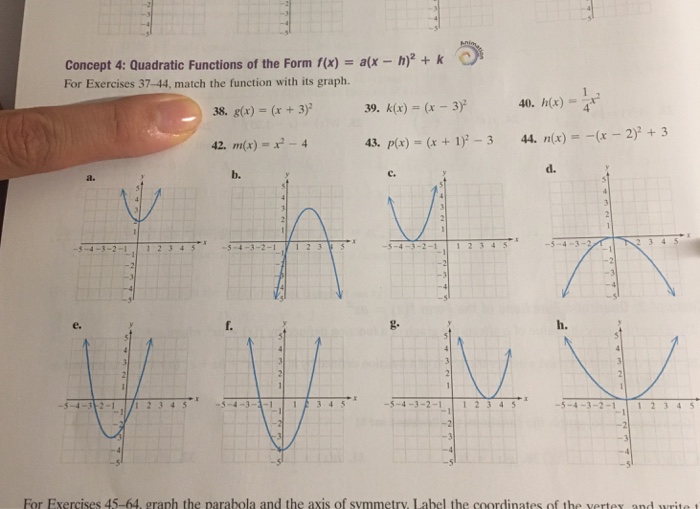



Concept 4 Quadratic Functions Of The Form F X Chegg Com



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora
Use the graph of the quadratic function f to write its formula as f(x)= a(x h)2 k f(x)= 6 a 4 G 8 14 112 2 24 62 Get more help from Chegg Solve it with A function is shown f (x) = 16x2 − 1 Choose the equivalent function that best shows the xintercepts on the graph arrow leftThe following applet allows you to select one of 4 parent functions The basic quadratic function f (x) = x^2 The basic cubic function f (x) = x^3 The basic absolute value function f (x) = x The basic square root function y = sqrt (x) In each of these functions, you will investigate what the parameters "a", "h", & "k" will do to the graph the parent function y = f (x) when we graph the function y = a*f (x h) k




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi



Y A X H 2 K Transformations
Learn how to graph just from using the vertex ordered pair and another ordered pair that the graph goes throughThe quadratic function f(x) = a(x − h)2 k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (b) If a >0=a (xh)2k No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation 0 (a* (xh)^2k)=0 Write the quadratic function in the form g (x)= a (xh)^2 k Write the quadratic function in the form g(x) = a(x−h)2 k https//mathstackexchangecom/questions//writethequadraticfunctionintheformgxaxh2k




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K Brainly Com
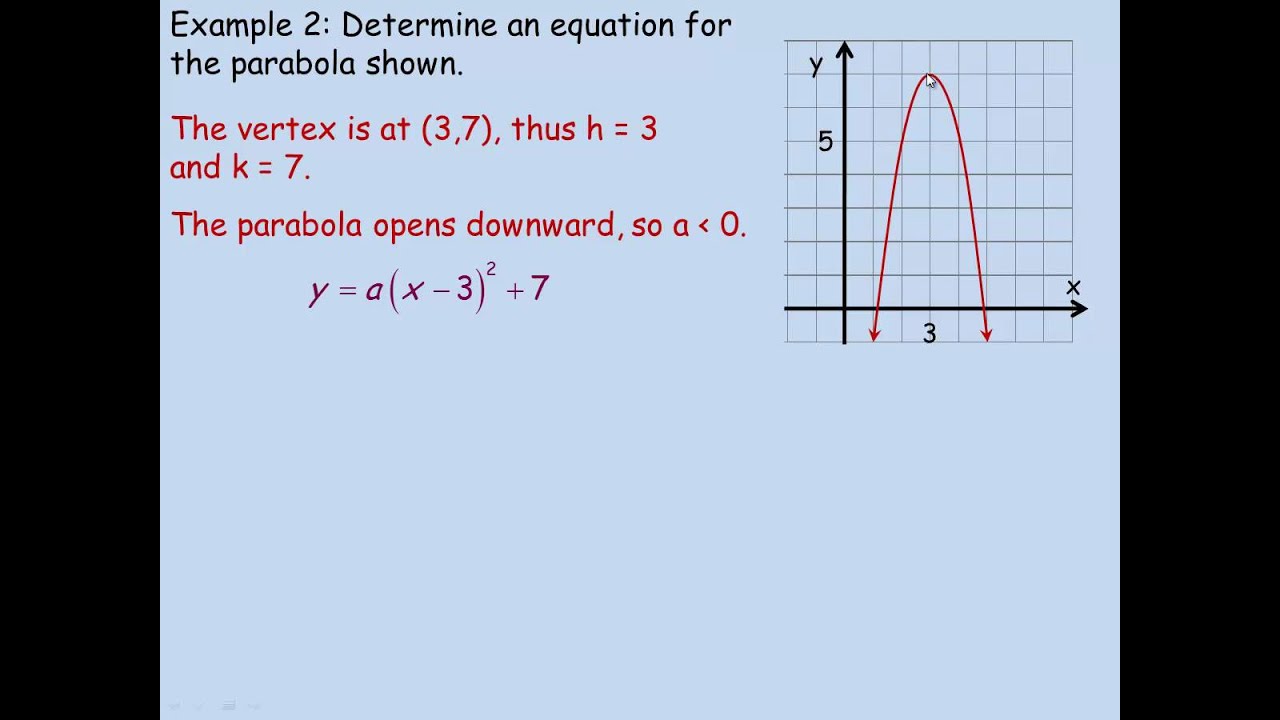



Graphing Y A X H K Youtube
The figure shows a graph of the function $f(x)=x^2$ a) For each of the graphs of quadratic functions below, find values of $a$, $h$, and $k$ so that the function $f(x) = a(x h)^2 k$ has that graph (For example, the graph in the first part corresponds to $a = 1$, $h = 0$, and $k = 0$)This video shows how to use vertex form ie y = a(x h)² k to graph a parabola or use it to write an equation from a graph This lesson was created foCalculus Q&A Library he quadratic function f(x)=a(xh)^2k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (_____) (b) If a > 0, the graph of f opens upward/downward In this case f(h) = k is the (maximum/minimum)value of f (c) If a < 0, the graph of f opens (upward/downward)




Quadratic Function Wikipedia



Illustrative Mathematics
Graph the function using transformations Graph a quadratic function in the vertex form f(x) = a(x − h)2 k using properties Rewrite the function in f(x) = a(x − h)2 k form Determine whether the parabola opens upward, a > 0, or downward, a < 0 Find the axis of symmetry, x = hQuestion Write the quadratic function in the form f(x)=a(xh)^2k Then, give the vertex of its graph f(x)=−2x^212x any help greatly appreciated Answer byA quadratic function f in vertex form is written as f (x) = a (x h) 2 k where h and k are the x and y coordinates respectively of the vertex (minimum or maximum) point of the graph The graph of of f is a parabola with the vertical line x = h as an axis of symmetry



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions




Quadratic Functions
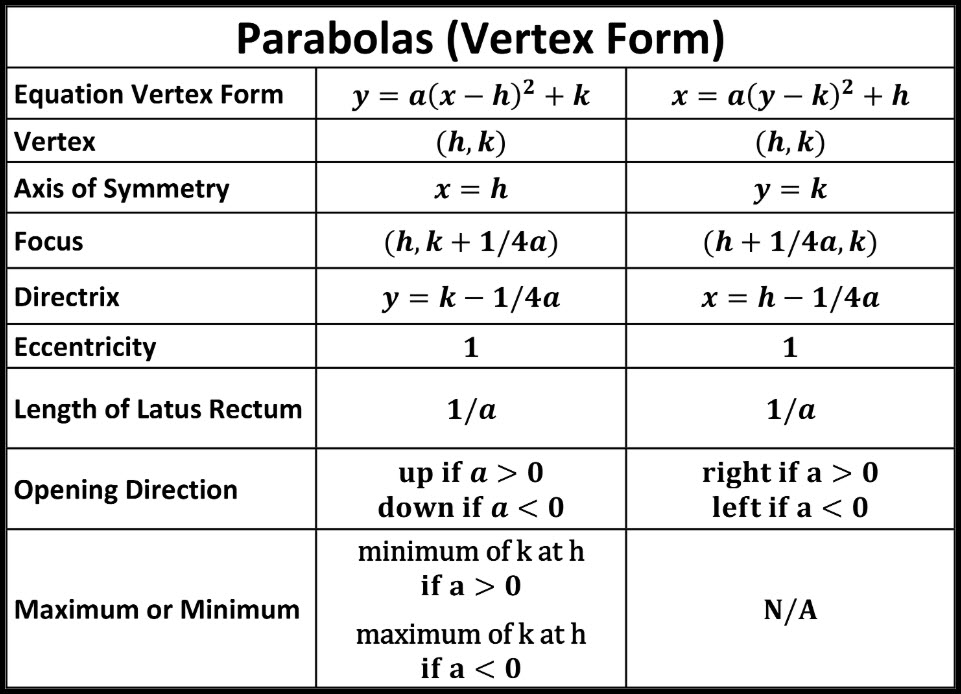
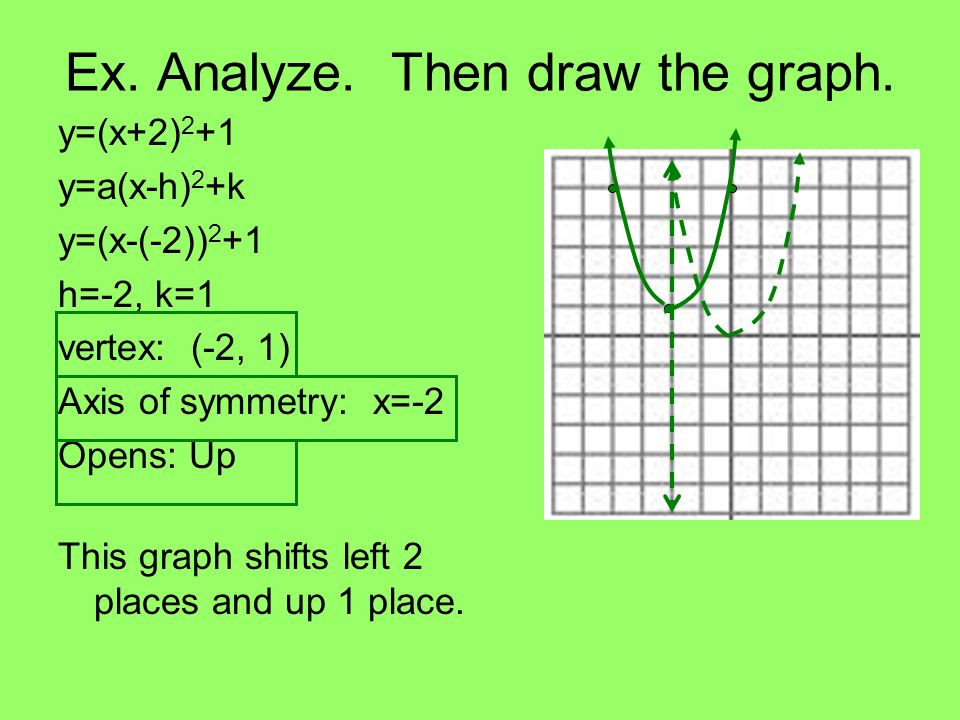
Notice that the main points on this graph are \(x = 2,\,1,\,4\) Graph of y = f(x) k Adding or subtracting a constant \(k\) to a function has the effect of shifting the graph up or downGiven a quadratic function f(x) = ax2 bx c with a≠0, completing the square can transform the function to the _____ form f(x) = a(x−h)^2 k The coordinates for the _____ are (h,k) f(h)=k is the _____ if a>0 and the _____ if aThe quadratic function f(x) = a(x h) 2 k, a not equal to zero, is said to be in standard form If a is positive, the graph opens upward, and if a is negative, then it opens downward If a is positive, the graph opens upward, and if a is negative, then it opens downward




Quadratic Functions Ppt Download
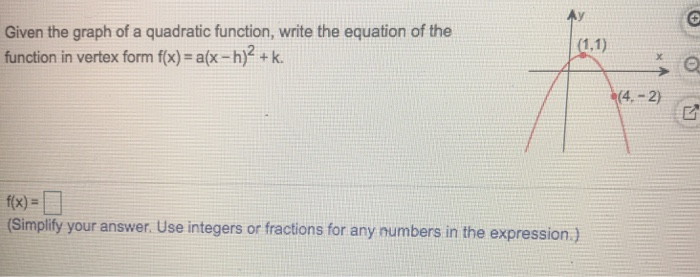



Given The Graph Of A Quadratic Function Write The Chegg Com
Precalculus (7th Edition) Edit edition Solutions for Chapter 31 Problem 2E The quadratic function f(x) = a(x−h)2 k is in standard form(a) The graph of f is a parabola with vertex (____, ____)(b) If a > 0, the graph of f opens _____ In this case f(h) = k is the _____ value of f (c) If a f opens Problem 22 Easy Difficulty Write the function in the form f ( x) = a ( x − h) 2 k by completing the square Then identify the vertex q ( x ) = −Write the quadratic function in the form f(x) = a(xh)2k Then, give the vertex of its graph f(x) = 2x² 16x28 Writing in the form specified f(x) = Vertex 00




Quadratic Functions




Quadratic Functions Ppt Download
SOLUTION Complete the square to write the function in f (x) = a (x − h)^2 k form Determine the vertex and the axis of symmetry of the graph of the function f (x) = −4x^2 Geometry Circles and their properties GeometryThe graph of f (x) = x h k contains the points (6, 2) and (0, 2) The graph has a vertex at (h, 5) Describe how to find the value of h Then, explain how this value translates the graph of the parent function Sample Response The absolute value function is symmetric with its vertex on the line of symmetryThe standard form makes it easier to graph Standard form looks like this f (x) = a(x h) 2 k, where a≠ 0 In standard form, h = and k = c The point (h, k) is called the vertex of the parabola The line x = h is called the axis of the parabola A parabola is symmetrical with respect to its axis The value of the function at h = k



Untitled Document



7 4 Transforming And Graphing Quadratics And Radicals Intermediate Algebra
How to graph quadratic functions in standard form or vertex form?Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with − 1 1 in the expression f ( − 1) = ( − 1) 2 f ( 1) = ( 1) 2 Simplify the resultSOLUTION Write the quadratic function in the form f (x)=a (xh)^2k Then, give the vertex of its graph f (x)=2x^2x52 Quadratics solvers Quadratics



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions




Shifting Parabolas Video Khan Academy
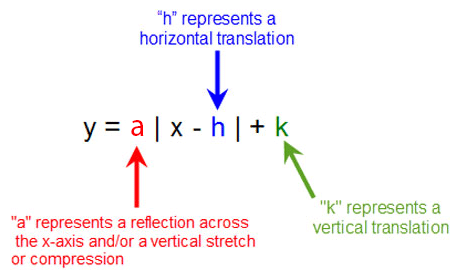
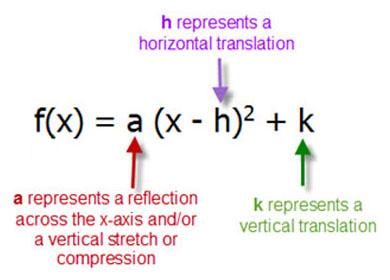
Question What do the values of a, h, and k in F(x)= a(xh)2 k telling you about the graph of the function compared to the graph of F(x) = x Give an example to illustrate your explanation Make sure to show the graph INSERT don t ATTACH0, the graph of f opens In this case f(h) = k is the value of f (c) If a <When written in "vertex form "• (h, k) is the vertex of the parabola, and x = h is the axis of symmetry • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0) • the k represents a vertical shift (how far up, or down, the graph has shifted from y = 0) • notice that the h value is subtracted in this form, and that the k value is added



Parabolas Andymath Com




Range Of Quadratic Functions Article Khan Academy
A quadratic function in the form f (x) = ax2 bxx f ( x) = a x 2 b x x is in standard form Regardless of the format, the graph of a quadratic function is a parabola The graph of y=x2−4x3 y = x 2 − 4 x 3 The graph of any quadratic equation is always a parabolaThe graph of y= Af B(xh) kis a transformation of the graph of y= f(x) The transformations can be done in the following order • A The function stretches or compresses vertically by a factor of A If A is negative, the function also reflects across the xaxis0, the graph of f opens In this case f(h) = k is the value of f please show step by step



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions
How to graph a quadratic function using transformationsParabolas The Vertex Form of a Parabola The formula for the vertex form of a parabola is f(x) = a(x h)2 k where a = vertical stretch or shrink of the parabola and (h, k) are the (x, y) coordinates of the vertex of the parabola h = the xcoordinate and k = the ycoordinateQuestion This question is from textbook solving quadratic functions of the form f(x)=a(xh)2k(that 2 is a squared) i know how to get the value of a,h,k, but i dont know what they mean when they say choose some values for x in example 1 they have 7 values for x, but in example 2 they have 5 values for x so how do you know how many numbers to chose forthe value of x?




Graph Quadratic Functions Using Transformations Intermediate Algebra



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
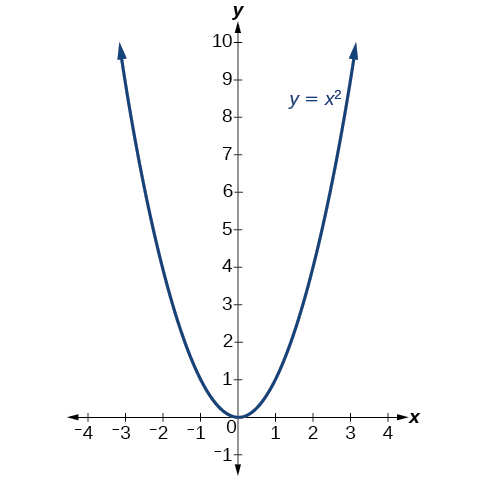
Algebra Graph f (x)=a (xh)^2k f (x) = a(x − h)2 k f ( x) = a ( x h) 2 k Graph f (x) = a(x−h)2 k f ( x) = a ( x h) 2 k(h, k) and a point on the graph (x, y) to find the general form of the equation of the quadratic function (h, k) = (−5, −1), (x, y) = (−7, 3) f(x) = _____ Found 2Graph Quadratic Functions Graphs of quadratic functions of the vertex form f(x) = a (x h) 2 k and of the standard form f(x) = a x 2 b x c are presented with several examples and their detailed solutions We start with the graph of the basic quadratic function f(x) = x 2, then we graph examples of quadratic functions in vertex form and then in standard form



Polynomial Functions Quadratic Functions Sparknotes




Quadratic Formula Calculator
Explore the parent graph y=x^3 Experiment with the values of a, h, and k What happens to the graph as these values change?LESSON 2 Graphing Quadratic Functions in Standard Form f(x)=ax^2bxcLESSON 3 Graphing Quadratic Functions in Vertex Form f(x)=a(xh)^2 kLESSON 4 Graphing Quadratic Functions in Intercept Form f(x)= a(xp)(xq)LESSON 5 Comparing and Graphing Quadratic Functions in Different Forms LESSON 6 Completing the Square of a Quadratic FunctionExample you have just plotted some interesting data, and it looks Quadratic Just knowing those two points we can come up with an equation Firstly, we know h and k (at the vertex) (h, k) = (1, 1) So let's put that into this form of the equation f (x) = a (xh)2 k f (x) = a (x−1)2
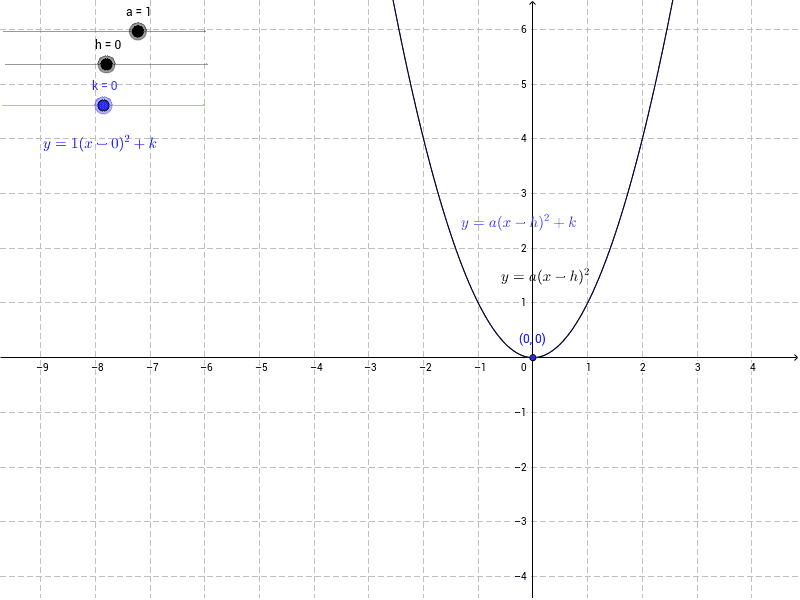



Investigating The Graph Of Y X H 2 K Geogebra



Graphing Quadratic Functions
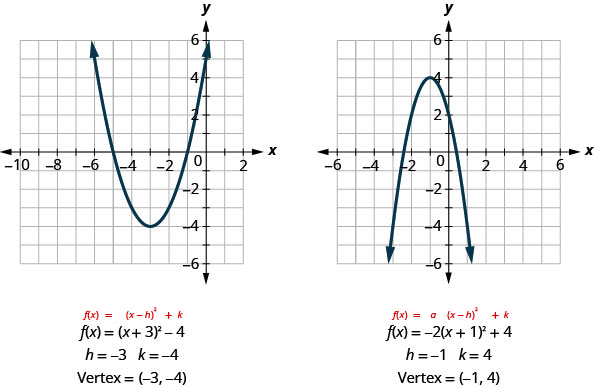
\f(x)=ax^2bxc \\ f(x)=2x^2−6x7\ Using the vertex to determine the shifts, \f(x)=2\Big(x–\dfrac{3}{2}\Big)^2\dfrac{5}{2}\ Analysis One reason we may want to identify the vertex of the parabola is that this point will inform us what the maximum or minimum value of the function is, \((k)\),and where it occurs, \((h)\)



Graphing Quadratic Equations In Vertex Form Walk Around Activity Lv 2 Scavenger




Unit 5 Quadratic Functions Flashcards Quizlet
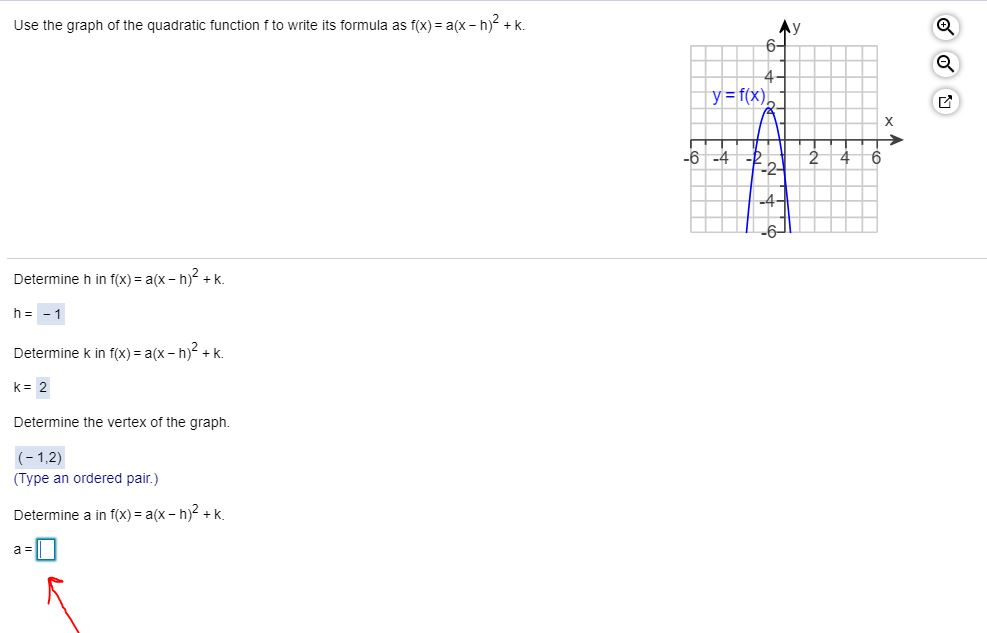



Use The Graph Of The Quadratic Function F To Write Chegg Com



Graph By Transformations F X A X H 2 K Youtube



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math




Quadratic Function Wikipedia




Quadratic Function
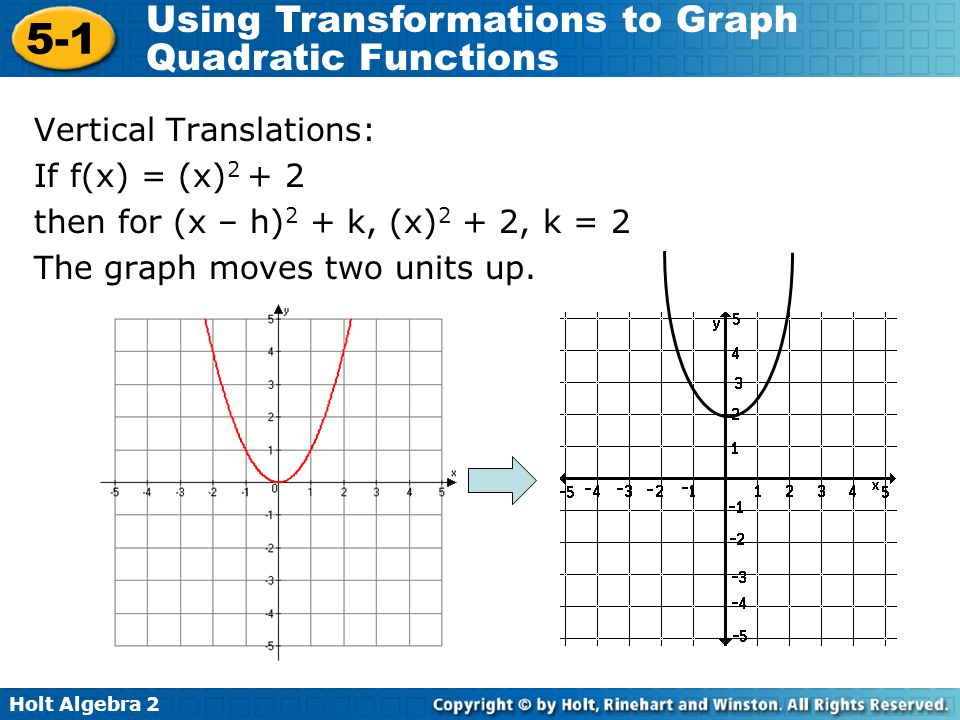



The Vertex Of The Parabola Is At H K Ppt Video Online Download




Graph F X X H 2 Youtube




Algebra Ii 9 5a Graphs Of F X A X H K Guidelines For Graphing Quadratic Functions Youtube




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip




6 6 Analyzing Graphs Of Quadratic Functions




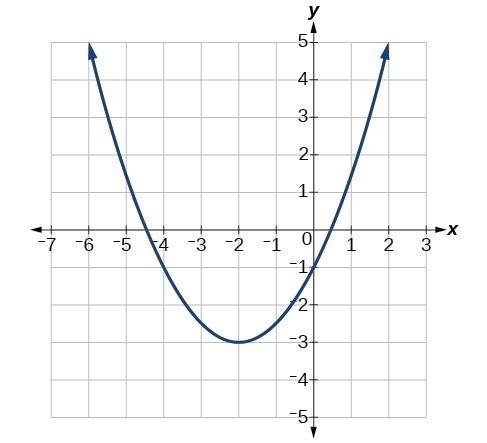
The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K What Is The Brainly Com
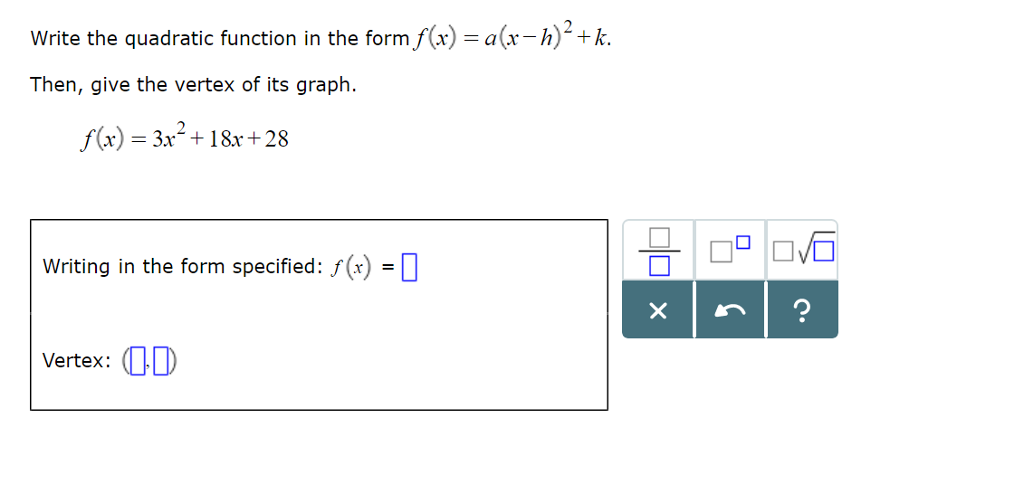



Write The Quadratic Function In The Form F X Chegg Com



6 6 Analyzing Graphs Of Quadratic Functions Ppt Download




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube



5 2 Quadratic Functions Mathematics Libretexts




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions



Graphing Quadratic Functions



9 8 Graph Quadratic Functions Using Transformations Mathematics Libretexts




Write The Quadratic Function In The Form F X Chegg Com




Determine The Quadratic Function Of The Form F X Chegg Com



Untitled Document



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf
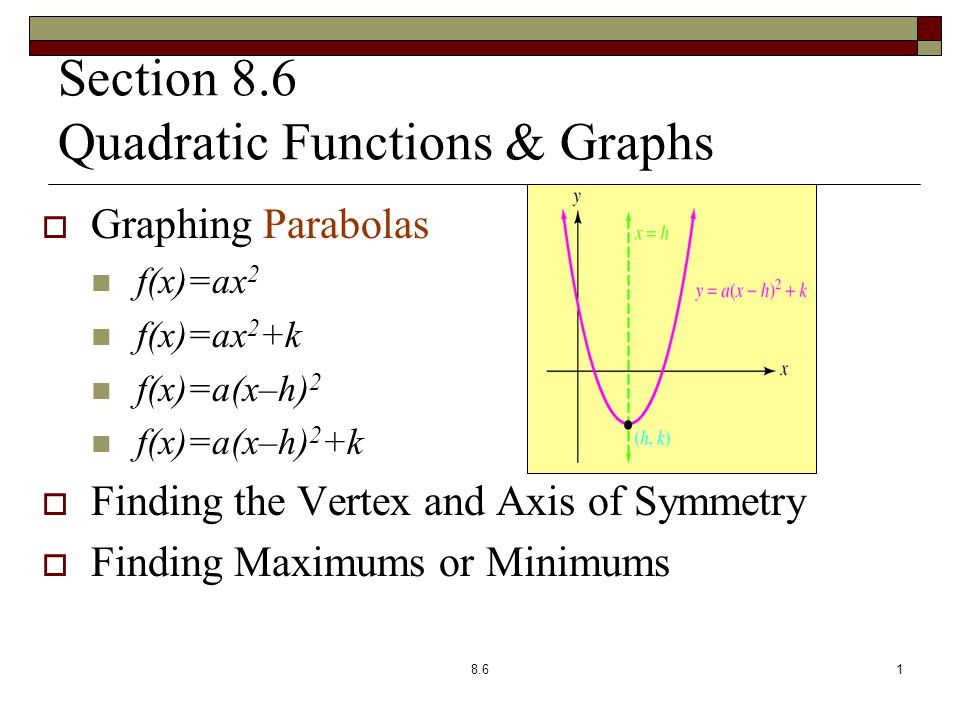



Section 8 6 Quadratic Functions Graphs Graphing Parabolas F X Ax 2 F X Ax 2 K F X A X H 2 F X A X H 2 K Finding The Vertex And Axis Of Symmetry Ppt Download



Solution The Graph Of F X X H K Contains The Points 6 2 And 0 2 The Graph Has A Vertex At H 5 Describe How To Find The Value Of H Then Explain How This Value Translates



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby



Www Hackensackschools Org Site Handlers Filedownload Ashx Moduleinstanceid 1615 Dataid Filename Vertex form transformations notes day 1 Pdf



Vertex Form Introduction Video Khan Academy




Graphing A Parabola In The Form Y X H 2 K Youtube



7 4 Transforming And Graphing Quadratics And Radicals Intermediate Algebra



7th Section 8 4 Graphing F X A X H 2 K Youtube



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



Graphing Quadratic Equations




How To Write Quadratic Functions Video Lesson Transcript Study Com



Y A X H 3 K Geogebra



1



Illustrative Mathematics




Quadratic Function




Answered Use The Graph Of The Quadratic Function Bartleby



The Quadratic Function F X A X H 2 K Is In Chegg Com



Solution Write The Given Expression In The Form F X A X H 2 K Identify The Vertex F X 6 5x 10x 2



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora
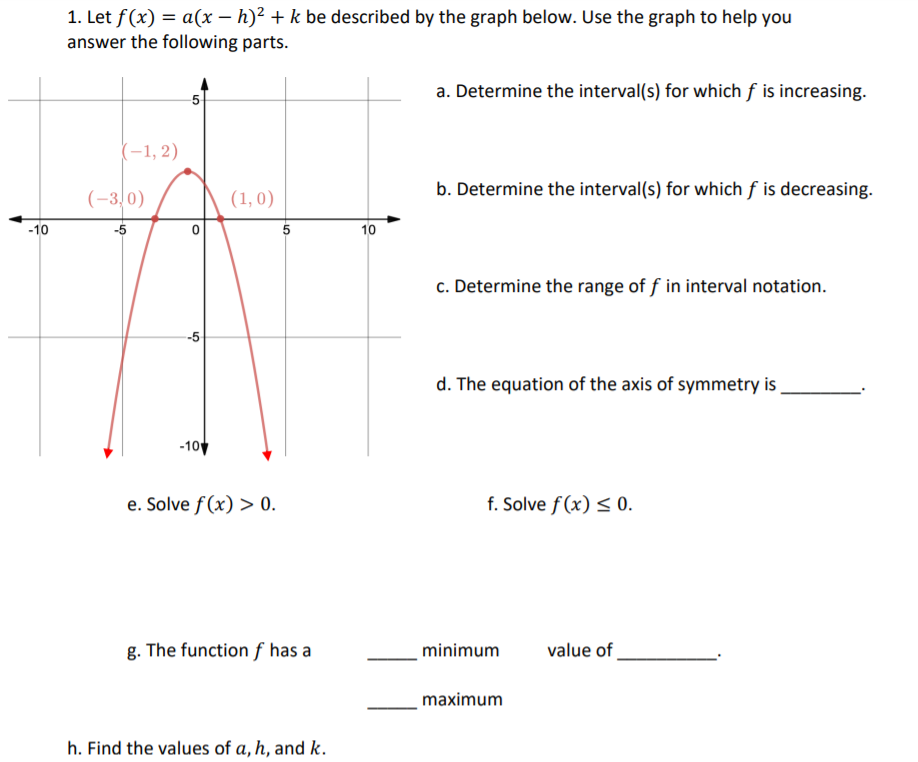



Let F X A X H 2 K Be Described By The Graph Below Chegg Com



A 8 4 Graphing F X A X H 2 K Youtube




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



7 4 Transforming And Graphing Quadratics And Radicals Intermediate Algebra



Transformations Of Graphs A H K Geogebra




How To Graph A Quadratic Equation 10 Steps With Pictures




8 4 Graphing F X A X H 2 K Youtube




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation
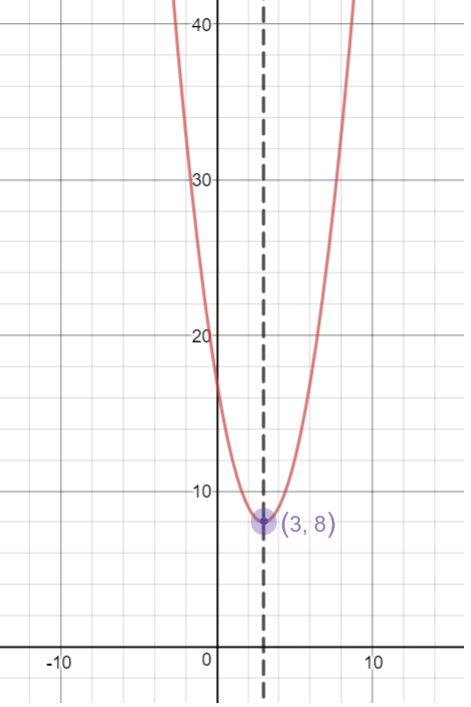



Vertex Form Of A Quadratic Equation Algebra Socratic




Also Identify The Vertex No Need To Sketch Write The Quadratic Function In A X H 2 K Form Hint Homeworklib
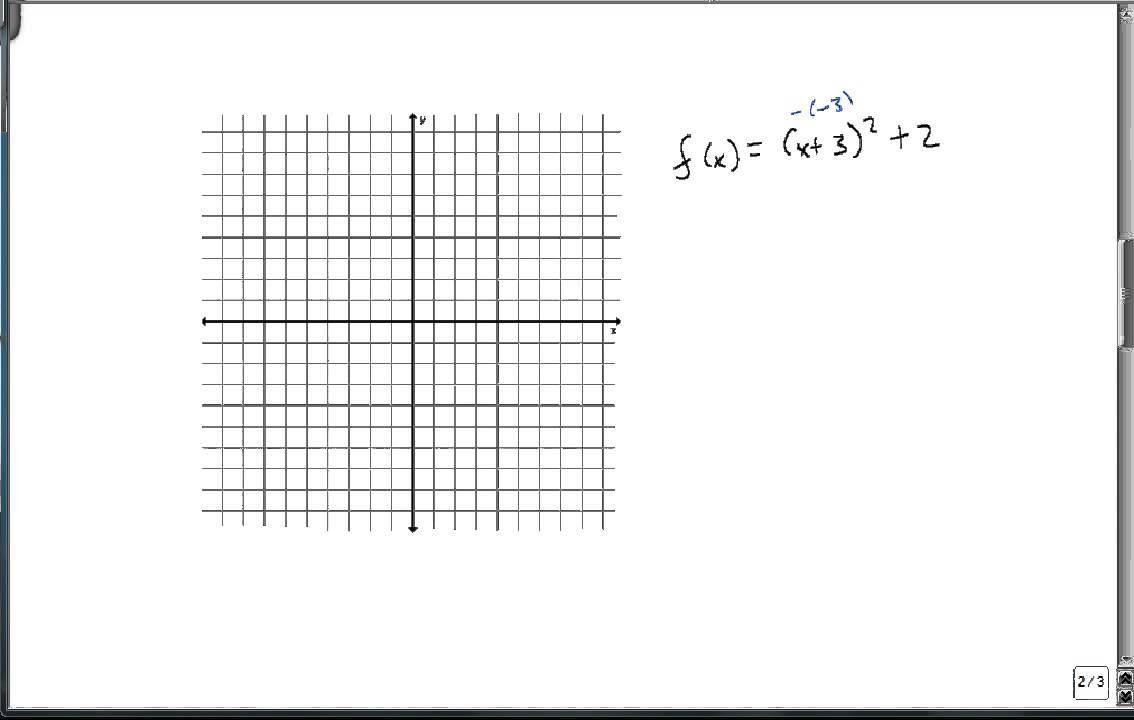



Graph F X X H 2 K Youtube



1




Finding Features Of Quadratic Functions Video Khan Academy




Algebra Ii 9 4 Graph F X Ax And F X A X H Youtube
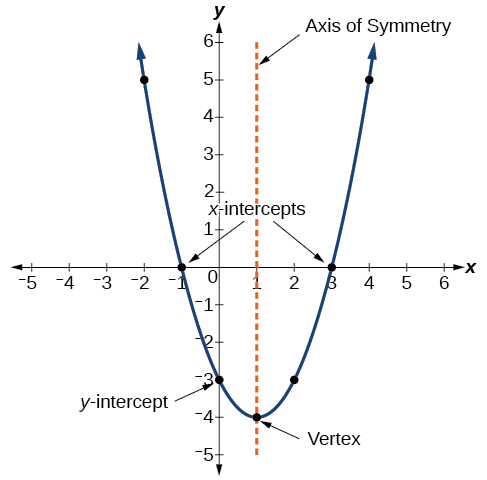



5 2 Quadratic Functions Mathematics Libretexts




The Graph Of F X X 2 Has Been Shifted Into The Form F X X H 2 K What Is The Value Of H A 1 B Brainly Com



Solved Use The Graph Of A Quadratic Function F To Write Its Formula As F X A X H 2 K F X Course Hero




Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown F X Brainly Com



Vertex And Intercepts




Transforming Quadratic Functions Study Com




The Graph Of F X Ax 2 All Quadratic Functions Have Graphs Similar To Y X 2 Such Curves Are Called Parabolas They Are U Shaped And Symmetric With Ppt Download



1
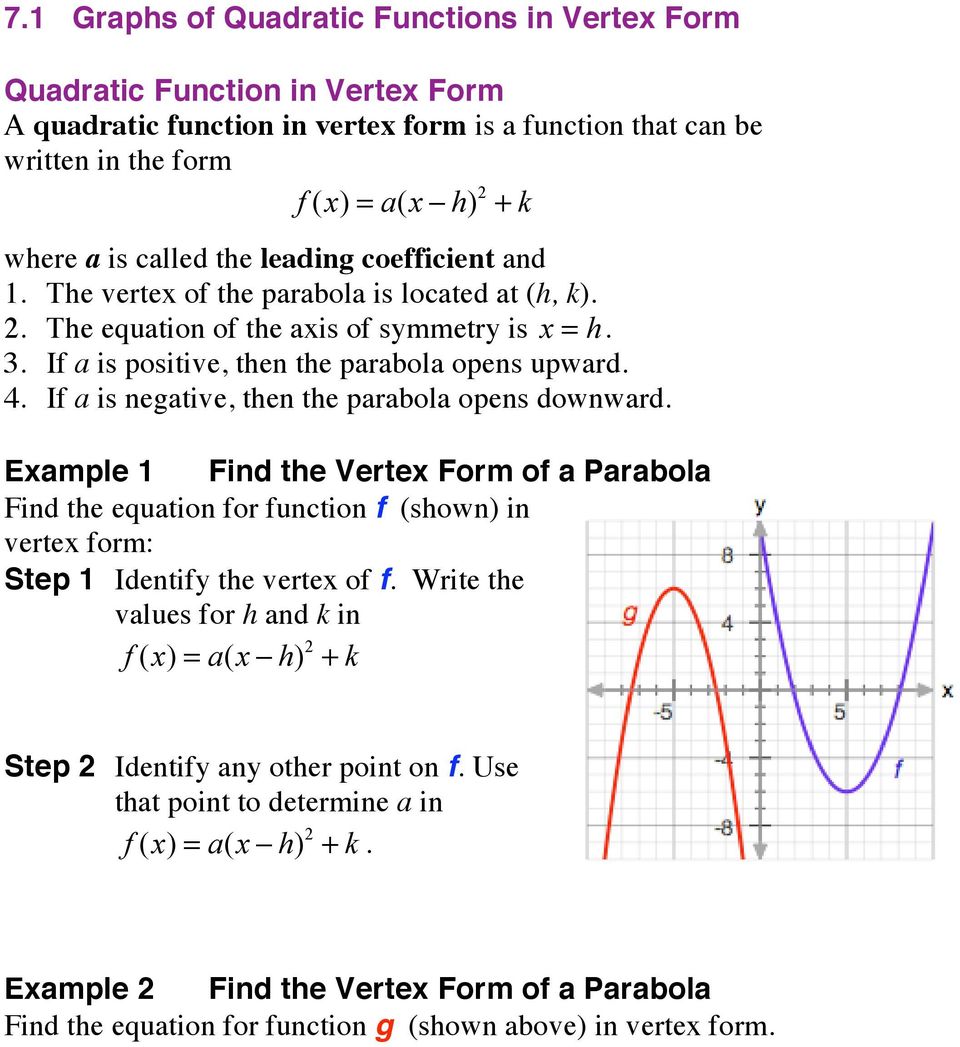



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola



Illustrative Mathematics




Quadratic Functions




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id




Graphing Quadratic Equations
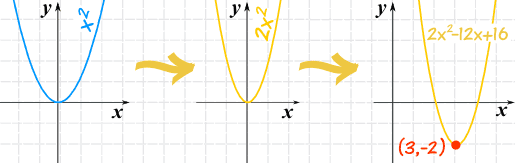



Graphing Quadratic Equations



Index Of Ojj Rcm27 Images



0 件のコメント:
コメントを投稿